債券価格と金利の関係（０） | 午後はカフェで経済学

金利の逆算

これから債券や金利の概念をいろいろ学んでいきます。「金利の逆算」はそのために必要な計算です。ここからは話を簡単にするため、複利計算は年１回としましょう。

まずは、金利から返済額を求める計算の復習です。たとえば金利5％、満期１年の約束で1000円借りたとすると、１年後の返済額は

$\begin{eqnarray*} \yen1000 \left(1 + 0.05\right) = \yen1050 \end{eqnarray*}$

です。同じ金利5％でも、満期5年の約束であれば、5年後の返済額は

$\begin{eqnarray*} \yen1000 \left(1 + 0.05\right)^5 = \yen1276\end{eqnarray*}$

ですね。

今日のテーマはその逆です。例えば「今日750円借りて、１年後1000円返さなければいけないとしたら、金利はいくらか」というのが今日のテーマです。この場合、求める金利を $x$ と置くと

$\begin{eqnarray*}\yen750 \left(1 + x\right) = \yen1000\end{eqnarray*}$

ですから、

$\begin{eqnarray*} 1+x &=& \frac{\yen1000}{\yen750}=1.3333\\ x &=& 0.3333 = 33.3\%\end{eqnarray*}$

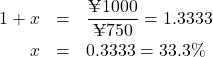
というのが正解です。今日750円受け取って、１年後に1000円返す場合の金利は「年率33.3%」です。

では、「今日750円借りて、５年後に1000円返す」という契約の金利はいくつでしょうか。この場合は、求める金利を $x$ と置くと

$\begin{eqnarray*}\yen750 \left(1 + x\right)^5 = \yen1000\end{eqnarray*}$

ですから、

$\begin{eqnarray*} \left(1 + x\right)^5 &=& \frac{\yen1000}{\yen750}\\ \left(1 + x\right)^5 &=& 1.3333\\ 1+x &=& \left(1.3333\right)^{\frac{1}{5}}\\ 1+x &=& 1.0592\\ x &=& 0.0592 = 5.92\% \end{eqnarray*}$

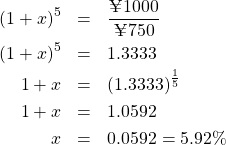
というのが正解です。今日750円もらって、５年後に1000円返す場合の金利は「年率5.92%」です。「５分の１」乗は、スマフォの電卓機能やエクセルでも簡単に計算できます。

金利が逆算できるようになったら、ファイナンスの最初の難関である、「債券価格と金利の関係」を勉強する準備が整います。つまずく人が多いテーマですが、ゆっくり着実に勉強していきましょう。

>> 債券価格と金利の関係（１）債券の売買とお金の貸し借り