複利計算（３）

<< （２）

複利計算の理論的なこと

前回までに、金利の複利計算式を勉強しました。今回はファイナンス理論に興味がある人が、複利計算について知っておくべき２つのことです。


１つ目は、「金利と貸借期間が同じなら、複利の頻度が多い契約ほど、返済額は大きくなる」ということです。 （なので、貸借契約をするときは、必ず複利の頻度がいくつかを確認してください。）試しに、年率５％の契約で１年間借りる場合に、複利の頻度によって返済額がどう違ってくるかを見てみましょう。

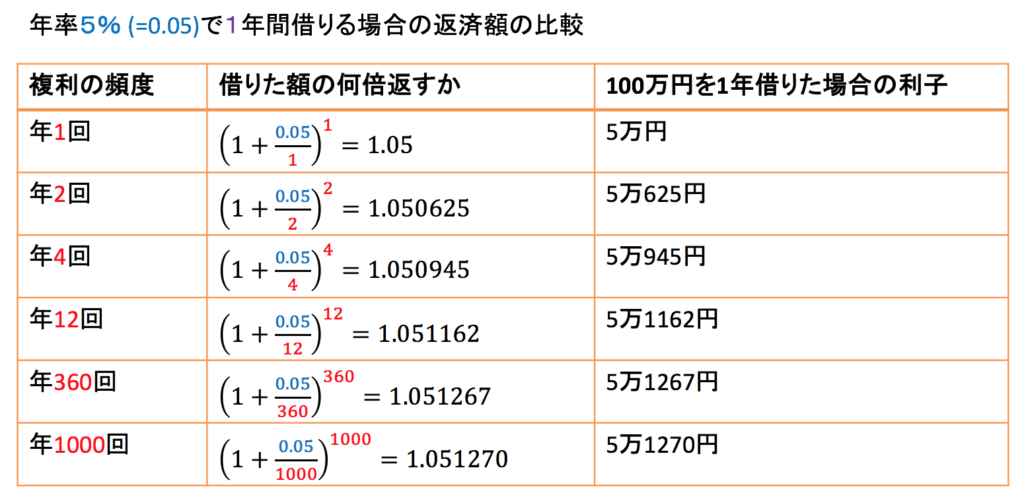
同じ100万円借りた場合でも、年１回複利の契約なら利子は5万円、年12回複利の契約なら利子は5万1162円ですから、同じ５％でも、複利頻度が大きいほど、利子が増えることがわかりますね。金利が20％なら、この差はもっと顕著になります。


理論として知っておくべきことの２つ目は、「複利頻度を年100回、1000回、10000回・・・と増やしても、返済額は際限なく大きくなったりはしない」ということです。このことを数学では「発散しない」とか「収束する」とか言います。


実際、年率５％で100万円を借りる場合、複利頻度が年１回から年12回に変わると返済額は1162円増えますが、12回から1000回に変わっても返済額はあと108円しか増えていません。複利の頻度を上げると返済額は上がるのですが、年何百万回に増やしても上がり続けることはなく、やがて「収束」します。際限なく大きくならない秘密は、複利計算の回数が倍になっても、そのぶん１回に適用される利率は半分になることが関係しています。


さて、金利の計算にもだんだん慣れてきたでしょうか。次回は借入額と返済額から、金利を「逆算する」練習をしたいと思います。