変数が3つ以上あるとき
2つの変数の関係の強さを教えてくれる相関係数。前回は、「英語の点数」と「数学の点数」という2つの変数の間の相関係数を、4人の学生のデータを使って計算してみました。
では英語、数学、音楽の3教科のテストの場合、話はどう変わるでしょうか。相関はあくまで2つの間の関係性の強さですから、3教科ある場合には「英語と数学の相関」、「英語と音楽の相関」、「数学と音楽の相関」というように、3つの相関が存在します。例として、前回の数値例に音楽のテストの成績も加えてみましょう。英語と数学の部分はまったく変わっていません。
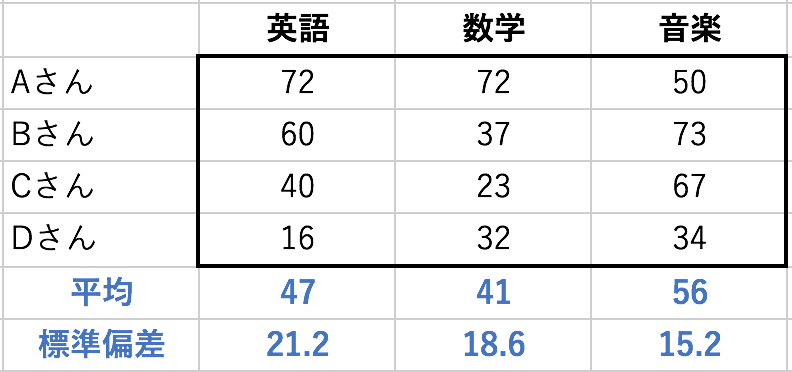
前回は、手計算で英語と数学の成績のあいだの相関係数0.71を求めました。英語と音楽の間の相関係数を求めるためにも、全く同じことをやります。ぜひ一度練習してもらいたいのですが、求めると0.52です。つまり、英語と音楽の間には、やや弱めの正の相関があるという結果になります。同様に、数学と音楽の間の相関係数を計算すると![]() です。4人の数学と音楽の点数を眺めているだけでは気づきませんが、弱い負の相関があることになります。まとめると、
です。4人の数学と音楽の点数を眺めているだけでは気づきませんが、弱い負の相関があることになります。まとめると、
英語と数学の相関:0.71
英語と音楽の相関:0.52
数学と音楽の相関:![]()
です。統計データを報告する研究発表や卒業論文では、相関係数を次のような表の形に並べます。
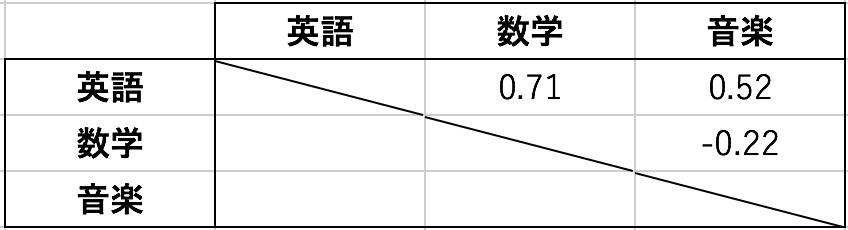
表では、縦にも横にも「英・数・音」を並べます。英語と数学の交わるところに0.71と書いてあるので、0.71が英語と数学の相関だと分かります。
4教科あれば6組、5教科あれば10組のペアが存在しますが、こんなふうに表を描いてやれば、相関係数をきれいに並べることができますね。相関係数を表の形に並べたものを、かっこよく「相関行列(そうかん・ぎょうれつ)」と呼んだりします。
次回のコラムでは、実際の研究において報告されている相関行列を紹介したいと思います。
>> 相関係数を知ろう(4)相関係数を調べた研究の例
