計算のしかた
簡単な数値例で相関係数を計算してみましょう。計算には標準偏差を使いますから、初めて聞く人は標準偏差についての過去のコラムを参照してください。
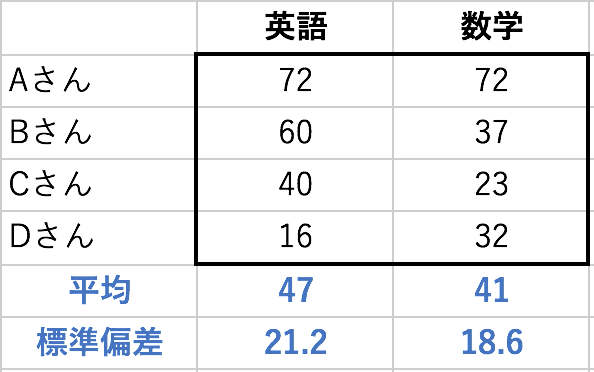
今4人の生徒の英語と数学の試験結果が、以下の表のようだったとします。英語の成績と数学の成績の相関係数を求めてみましょう。
相関係数を計算するための手順は4つです。
手順1:4人の平均点と標準偏差を、英語と数学それぞれについて計算する
手順2:各人、「英語の平均からのギャップ」と「数学の平均からのギャップ」を求める
手順3:各人、2つのギャップの積を求め、その積の4人の平均を計算する
手順4:最後に、数学の標準偏差と英語の標準偏差で割る
となります。まず4人の英語の平均は![]() 点、標準偏差は計算方法は省略しますが、21.2点です。一方数学の平均は
点、標準偏差は計算方法は省略しますが、21.2点です。一方数学の平均は![]() 点、標準偏差は18.6点です(手順1)。これらの数字は表にも載せておきました。
点、標準偏差は18.6点です(手順1)。これらの数字は表にも載せておきました。
次に、4人それぞれの「平均点からのギャップ」は英語ではそれぞれ![]() 点、数学ではそれぞれ
点、数学ではそれぞれ![]() 点です(手順2)。
点です(手順2)。
したがって、英語の平均からのギャップと、数学の平均からのギャップの積は、Aさんが![]() , Bさんが
, Bさんが![]() , Cさんは
, Cさんは![]() , Dさんは
, Dさんは![]() ですので、これの平均は
ですので、これの平均は![]() です(手順3)。
です(手順3)。
最後にこれを英語と数学それぞれの標準偏差で割って![]() となり、これが英語の成績と数学の成績の間の相関係数となります(手順4)。
となり、これが英語の成績と数学の成績の間の相関係数となります(手順4)。
0.71はそれなりの相関です。英語の能力と数学の能力の間にはそれなりの強さの正の相関があるという結果になりました。
理論的なポイントは、手順3で「数学の平均からのギャップ」と「英語の平均からのギャップ」の積を求めているところです。英語も数学も平均より高い人や、両方とも平均より低い人は、この積がプラスになります。一方、英語は平均を上回ったけど数学は平均を下回った、というような人は、この積がマイナスになります。したがって両教科ともできた人や、両方ともできなかった人が多いと、相関係数はプラスになり、片方の教科だけできた人が多いと、相関係数はマイナスになるのです。
手順4は、相関係数が魔法のように必ず1と![]() の間にぴたっと収まるための、最後の仕上げのような手順なのですが、そのからくりは省略します。
の間にぴたっと収まるための、最後の仕上げのような手順なのですが、そのからくりは省略します。
さて、上の例では英語と数学の2教科しかありませんでしたが、テストの教科数が3つ以上あったら、相関係数はどうなるのでしょうか。難しい話ではないのですが、次回はその話をしたいと思います。
>> 相関係数(3)変数が3つ以上あるときの相関係数
