<<(1)
例2.期待値
経済学に出てくるベクトルと内積の例をもうひとつ挙げます。
今、ある宝くじの1等から4等ハズレまでの各確率が1等は 5%(=0.05),2等は10%(=0.1),3等は20%(=0.2),4等は65%(=0.65)であるとしましょう。確率 (probability) の頭文字をとってこれを
![]()
と書くことにします。確率が4つあるのでそれを並べただけですが、経済学ではこれを「確率ベクトル」と呼びます。
一方、この宝くじの当選金は、1等が10万円、2等が5万円、3等は2万円、4等ハズレでも1万円、という設定とします。すると「当選金ベクトル」は、お金 (money) の頭文字をとって
![]()
と表わすことができます。
このくじの当選金の期待値はいくらでしょうか。期待値は当選金とそれに対応する確率を各々かけあわせて、最後に足し合わせたものでしたね。勘のいい人はもうお気づきかもしれませんが、これは
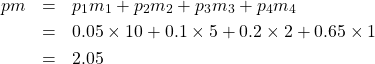
で、答えは2.05万円となります。
この例の確率変数は賞金ですが、とくに賞金である必要はありません。気温、点数、株価、なんでもOKです。期待値は、確率のベクトルと実現値のベクトルとの、内積だと理解してください。
次回は加重平均です。確率の代わりに、確率と同様、合計が1になるような「加重(ウェイト)」を表すベクトルを使って内積を計算します。
>> 経済学におけるベクトルと内積(3)例3.加重平均
