<< （１）

下準備


「カラテ・キッド」という1984年のアメリカ映画があります。いじめられっ子の主人公ダニエル君が、空手の達人ミスター・ミヤギに弟子入りするのですが、毎日やらされるのは「車のワックスがけ」や「塀のペンキ塗り」ばかり。見習いの登竜門だと思って辛抱していたダニエル君ですが、しまいには堪忍袋の尾が切れます。しかし、実は全てが空手の動きを習得するための修行だったのです。それがダニエル君に明かされる場面は、気分がスカッとする人気のシーンです。


今回はみなさんに、ダニエル君になってもらわなくてはなりません。目標は「クーポン債の価格理論」ですが、今回は全く関係なさそうな「算数の文章題」や「中学の連立方程式」の話をします。それでも飛ばさずに、辛抱して目を通してください。全てはクーポン債の理論のためだったことが、遅かれ早かれ明らかになるはずです。


１問目
リンゴが１個0.98ドル、バナナが１本0.96ドル、みかんが１個0.94ドルだとします。リンゴ10個、バナナ10個、みかん110個が入った詰め合わせセットの値段はいくらになるか答えなさい。


解答
式は

    \begin{eqnarray*} \$0.98 \times 10 + \$0.96 \times 10 + \$0.94 \times 110 = \$122.8 \end{eqnarray*}


となります。よって答えは122.8ドルです。経済学では、特に断りがない限り、まとめ買いすることによって割安になったりしません。それぞれの単価に個数をかけて合計するだけです。


２問目
今、詰め合わせセットが３種類売られていて、市場でついている価格は
・セット１が「リンゴ101個」で98.98ドル
・セット２が「リンゴ3個、バナナ103個」で101.82ドル
・セット３が「リンゴ2個、バナナ2個、みかん102個」で99.76ドル
です。このとき、リンゴ、バナナ、みかんそれぞれの単価を求めなさい。


解答
リンゴ１個、バナナ１個、みかん１個の値段をそれぞれx_1ドル、x_2ドル、x_3ドルとすると

    \begin{eqnarray*} \left\{ \begin{array}{rrrrrrr} 101x_1& & &&& =& 98.98\\3x_1 & + &103x_2 & & &=&101.82 \\ 2x_1 & + & 2x_2 & + & 102 x_3 & =& 99.76 \end{array}\right. \end{eqnarray*}


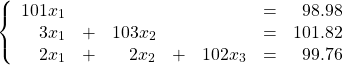
という連立方程式が立ちます。たとえば２番目の式の意味はこうです。リンゴが１個x_1ドル、バナナが１個x_2ドルならば、リンゴが3個、バナナが103個入っているセット２の値段は3x_1 + 103 x_2です。市場でついている値段101.82はこれに等しいはずですね。残りの２つの式も同じように解釈してみてください。


この連立方程式を解くと、(x_1, x_2, x_3)=(0.98, 0.96, 0.94)です。１つめの式からx_1が求まるので、それを２つめの式に代入すれば、x_2も求まります。そうやって順番に求めていくと、リンゴは１個0.98ドル、バナナは１個0.96ドル、みかんは１個0.94ドルだということになります。


さあ、これでワックスがけもペンキ塗りも終わりです。次回からは本当にクーポン債の価格理論に入ります。

>> クーポン債の理論（３）クーポン債は、割引債の詰め合わせセット


リメイク版もありますが、やはりオリジナルがお薦めです。