<<(2)
例3.加重平均
前回は「期待値」を内積として計算しました。今回は、「加重平均」を内積で計算してみます。
たとえば、80点、60点、40点を取った生徒の割合がそれぞれ![]() ,
, ![]() ,
, ![]() である場合の、平均点を考えてみましょう。それぞれの点数を取った生徒の割合 0.5, 0.3, 0.2を重み(ウェイト)として加重平均を取ればいいので、平均点は
である場合の、平均点を考えてみましょう。それぞれの点数を取った生徒の割合 0.5, 0.3, 0.2を重み(ウェイト)として加重平均を取ればいいので、平均点は
80点 × 0.5 + 60点 × 0.3 + 40点 × 0.2 = 66点
です。ここで、重みも確率と同様に合計が1になるので、加重平均も期待値と全く同じように、2つのベクトルの内積で表せます。すなわち、点数(score)のベクトルと重み(weight)のベクトルをそれぞれ
![]()
と置けば、クラスの平均点は
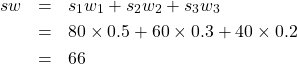
です。
ファイナンスへの応用
ファイナンスで習う、「ポートフォリオの収益率」は加重平均の一例です。今、A, B, Cという3つの株式銘柄で構成されたポートフォリオの収益率を考えてみましょう。それぞれの収益率は、![]() ,
, ![]() ,
, ![]() だったとしましょう。収益率はReturnの頭文字をとって
だったとしましょう。収益率はReturnの頭文字をとって![]() で表しています。今、投資資金のうち、5割を株式A、3割を株式B、2割を株式Cに投資したポートフォリオを考えます。個別銘柄の収益率のベクトルと、ポートフォリオへの組み入れ比率のベクトルはそれぞれ
で表しています。今、投資資金のうち、5割を株式A、3割を株式B、2割を株式Cに投資したポートフォリオを考えます。個別銘柄の収益率のベクトルと、ポートフォリオへの組み入れ比率のベクトルはそれぞれ
![]()
となります。
ここでは詳細は省略しますが、ポートフォリオの収益率は、個々の銘柄の収益率を、ポートフォリオ組み入れ比率を使って加重平均したものです。内積で表すことができて
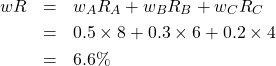
が答えとなります。
内積の計算に慣れたら、次は「行列の掛け算」を勉強してみましょう。
