例1.合計の支出
高校ではベクトルを、物体の運動という物理的なイメージで教えます。でも、経済学のベクトルはもっと単純です。経済学では、数字が2つ以上並ぶものを何でも「ベクトル (vector)」と言います。
例えばリンゴの値段が100円、バナナの値段が200円、ココナッツの値段が400円であるとしましょう。これらの値段をずらっと並べたもの ![]() を「価格ベクトル」と呼んだりします。ベクトルの意味は、「数字が2つ以上並んでいるよ」というだけの意味です。価格 (Price)、リンゴ (apple)、バナナ (banana)、ココナッツ (coconut)の頭文字をとって、それぞれのフルーツの価格を
を「価格ベクトル」と呼んだりします。ベクトルの意味は、「数字が2つ以上並んでいるよ」というだけの意味です。価格 (Price)、リンゴ (apple)、バナナ (banana)、ココナッツ (coconut)の頭文字をとって、それぞれのフルーツの価格を![]() ,
,![]() ,
,![]() と表すことにすれば、「リンゴは100円、バナナは200円、ココナッツは400円です」という代わりに、「リンゴ、バナナ、ココナッツの値段は
と表すことにすれば、「リンゴは100円、バナナは200円、ココナッツは400円です」という代わりに、「リンゴ、バナナ、ココナッツの値段は
![]()
というベクトルで与えられている」という言い方をします。
高校ではベクトルは文字の上に矢印をつけて、
さて、今リンゴ、バナナ、ココナッツをそれぞれ10個、5個、3個買うことを考えましょう。数量は英語でQuantityですから、今その頭文字をとって購入する数量のベクトルを
![]()
と書き表すことにします。単価と購入量が決まれば合計の出費が計算できますが、いくらになるでしょうか。答えは、単価と数量をそれぞれ掛けたあと、足し合わせればいいので、
![]()
ですね。2つのベクトルがあるとき、1番目の数字どうしを掛け、2番目の数字どうしを掛け・・・として最後に足し合わせる演算を「内積(ないせき)」と言います。つまり「価格ベクトル」と「数量ベクトル」が与えられたら、合計の支出は2つのベクトルの内積に他ならないのです。経済学では単純に
ちなみに、エクセルで内積を求めるときは、「積の和」を意味するSUMPRODUCTという関数を使います。以下の図のように、2つのベクトルの範囲を、コンマで区切って与えてやるだけです。
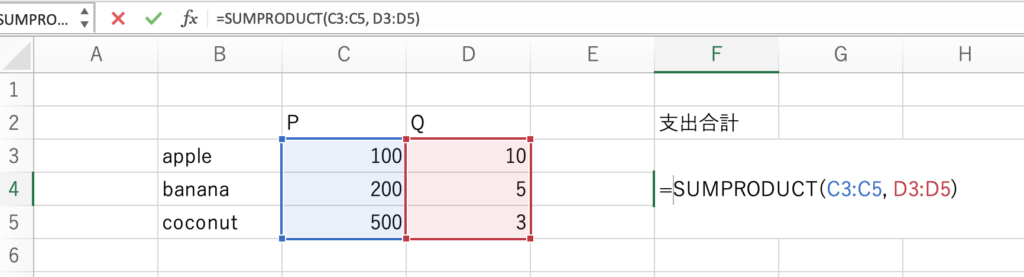
これで3500という答えが出てきます。ベクトルの内積に慣れるため、次回は別の例を紹介します。
>> 経済学におけるベクトルと内積(2)例2.期待値
