<<(3)
中間財でも最終財でもある「金属」と「機械」の例
前回の設定では小麦とパンの2財があり、小麦は小麦自身を作るためにも、パンを作るためにも必要な中間投入でした。一方でパンが中間投入になることはありませんでした。そこで今度は、2つの財のどちらも中間投入になる場合を解いてみましょう。
例題3
金属と機械の2種類の財しか存在しない世界を考える。今、ある国には「色々金属」と「様々機械」という名前の2つの企業しか存在しないとする。色々金属社は1億円分のいろいろな金属を生産するための中間投入として、0.1億円分のいろいろな金属を使い、0.2億円分のさまざまな機械を新しく導入する必要がある。一方の様々機械社は、1億円分のさまざまな機械を生産するための中間投入として、0.3億円分のいろいろな金属を使い、0.5億円分のさまざまな機械を導入する必要がある。これらの“レシピ”は以下の表にまとめられる。

2017年、この国の粗生産(中間投入に使われる分と最終需要に使われる分の合計)は、いろいろな金属が300億円分、さまざまな機械が500億円分だったという。
問1:最終需要を満たすのに使われた分の金属と機械はそれぞれ何億円分か。
問2:金属産業と機械産業それぞれが生み出した付加価値はいくらか。
ちなみに、小麦や金属のように、原材料として使ったらなくなってしまうものと違い、ふつうは機械は何年も使い続けられるので、原材料という扱いをしないのですが、この例題では機械も一度使ったらなくなってしまう原材料だと考えてください。
問1の解答
問1は次の表を埋めながら考えていきます。
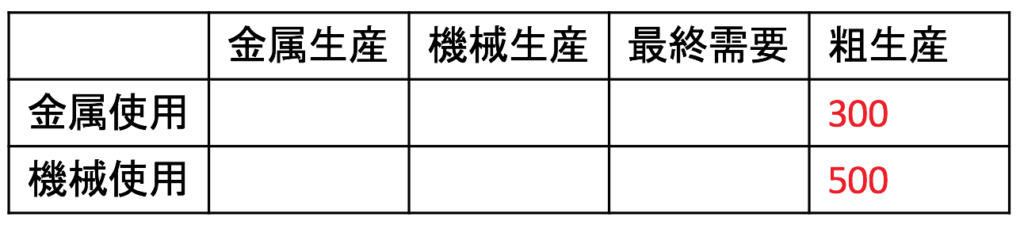
300億円分の金属を作るために必要な金属は![]() 億円分、500億円分の機械を作るために必要な金属は
億円分、500億円分の機械を作るために必要な金属は![]() 億円分です。機械についても同じように考えます。300億円分の金属を作るために必要な機械は
億円分です。機械についても同じように考えます。300億円分の金属を作るために必要な機械は![]() 億円分、500億円分の機械を作るために必要な機械は
億円分、500億円分の機械を作るために必要な機械は![]() 億円分です。
億円分です。
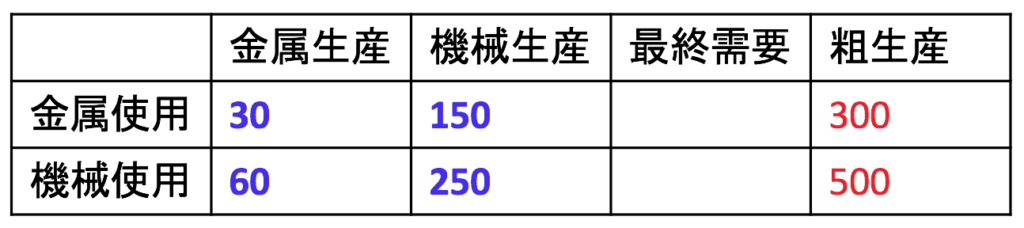
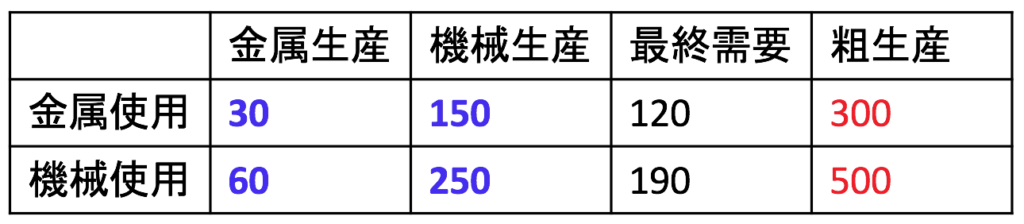
中間投入に消える金属は計180億円分なので、残り120億円分が最終消費に使われる金属です。中間投入に消える機械は計310億円分なので、残り190億円分が最終消費に使われる機械です。
式の方が分かりやすいという人のために、文字で表しておきます。粗生産は金属を![]() , 機械を
, 機械を![]() と置き、最終需要は、金属を
と置き、最終需要は、金属を![]() , 機械を
, 機械を![]() と置くと、
と置くと、
金属:![]()
機械:![]()
となります。![]() ,
, ![]() ということなので、
ということなので、![]() ,
, ![]() が出てきます。式中での各項の位置が、表の各項目の位置と完全に一致しています。
が出てきます。式中での各項の位置が、表の各項目の位置と完全に一致しています。
問2の解答
それでは問題の後半、各産業の貢献(その産業の労働者や資本家の生み出した付加価値)を計算しましょう。以下の表を埋めていくかたちで求めます。
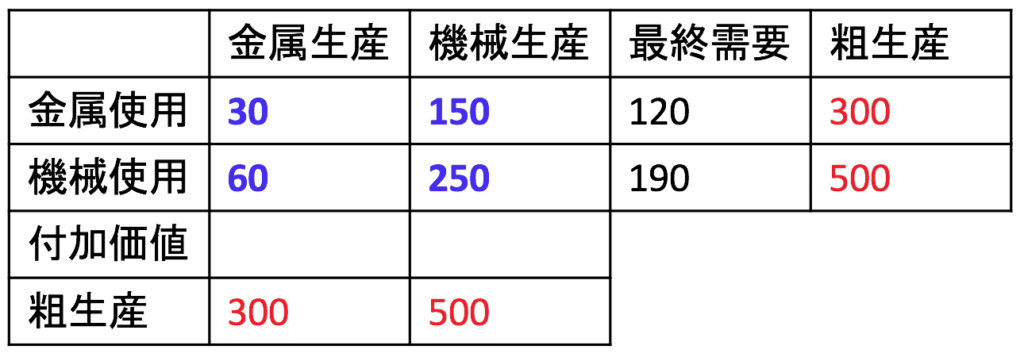
その産業が作った物の総額から、原材料の価値を差し引いたものが、その産業の貢献です。
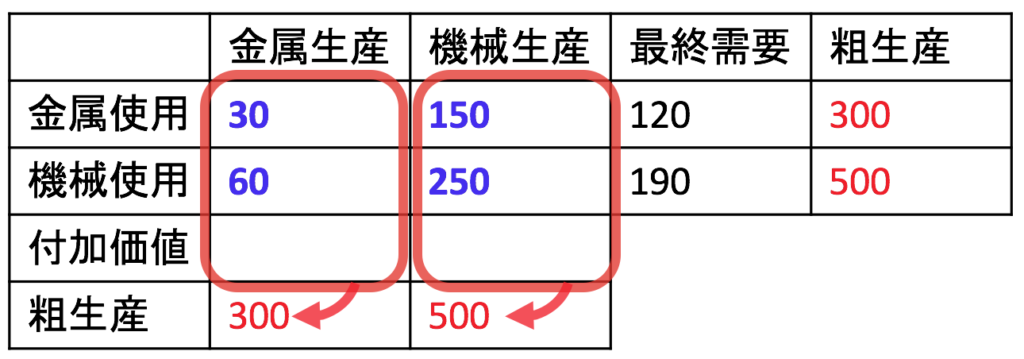
金属産業は、30億円分の金属と60億円分の機械を原材料として使って300億円分のものを生み出したので、付加価値は差額の210億円分です。機械産業は150億円分の金属と250億円分の機械を原材料として使って500億円分のものを生み出したので、付加価値は差額の100億円分です。
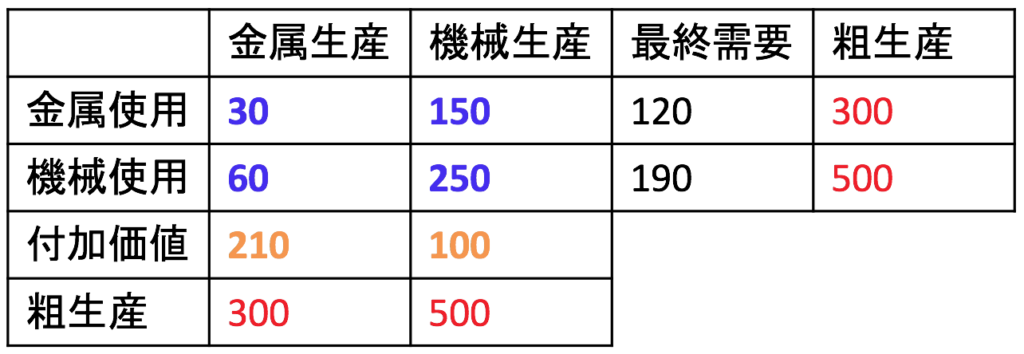
合計は310億円で、最終需要の合計と等しくなりますね。「付加価値」と「最終需要」は合計では310億円で等しくなります。この国が生み出したGDPは310億円です。
終わりに
いかがでしたか。ここで全4回の内容を締めくくりたいと思います。何がどれだけ作られたかを考えるときは「中間投入」を差し引く必要があります。原材料の二重計算を防ぐためです。そのためのレオンチェフのアイディアはこうです。まず、「各財の生産に中間投入がどれだけ必要か」という“レシピ”を、あらかじめ過去の経験から推定し、表にしておきます。このページの一番最初の表がそれです。あとは、各省庁の統計が、今年の各財の粗生産を教えてくれるので、この例題の方法で中間投入を差し引きます。出来上がりの最後の表を見れば、原材料を引いた最終需要の内訳は一目瞭然です。
ここでは財と産業の数が2つの場合を考えましたが、3つでもN個でも考え方は同じです。でもその話題はまたの機会にして、次回からはケインズ風の政策を考えるための、有名な「45度線モデル」を勉強しましょう。
>> GDPの45度線モデル(1)イントロ
